최고로 기본적인 분산과 표준편차는 왜 이리 잘 까먹는지 모르겠다....
분산과 표준편차의 의미 :
평균에서 얼마나 많이 떨어져 있는가?
즉 모집단에서 이질적인 성질을 가진 놈이 어떤 놈이고 어떤 기준으로 할것인가?를 찾아 내는 수학적
기법으로 값이 작을 수록 동질적인 성향이 짙고(조밀하고) 값이 클수록 이질적인 성향이
짙다( 흩어져 있다.)라고 할수 있다.
어떤 모 집단에서 이질적인 대상을 찾기 위해 모집단의 평균과 표준편차를 이용하면 되는데 여기서 분산을 사용하지 않는 이유는
분산은 평균과 객체간 차이의 제곱값을 이용하기 때문에 실제값과 유사성이 떨어지지만
표준편차는 분산(평균과 객체간 차이의 제곱값 )의 제곱근 이기때문에 실제 값과 강한 유사성을 가지고 있기 때문이다.
평균 :
Mean, average
자꾸 까먹는 분산, 표준편차의 의미와 공식
개들의 키 : 430mm와 300mm 600mm, 470mm, 170mm.
산술 평균 : 430 + 300 + 600 + 470 + 170 / 5 = 394
분산 :
σ^2 또는 var ( variance )
제곱을 해 주는 이유는 평균에 대한 양 / 음 차이를 좀더 편리하게 계산 하기위함.
표준편차 :
분산( σ^2 )의 제곱근 또는 sigma
표준 편차 : σ = √ 21704 = 147.32 ... = 147
즉 , 평균에서 147보다 크거나 작으면 친밀함/유사성 ??이 좀 떨어지는
경우라고 볼수 있겠지...
- ]
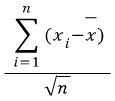
샘플 데이텨가 적을 경우에는 N=N-1로 한다
'수학이론 일반 ' 카테고리의 다른 글
| [ partial differentiation , 偏微分 ] (0) | 2016.11.04 |
|---|---|
| 1. 복리수익률을 최대화하는 켈리 기준(Kelly Criterion) 유도 (0) | 2016.05.26 |
| 기본 공식 General Formula (0) | 2016.04.28 |



